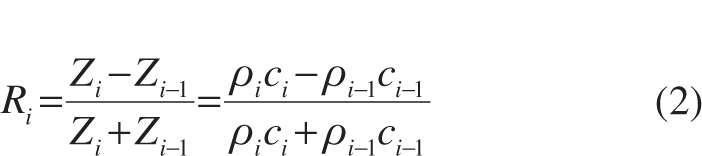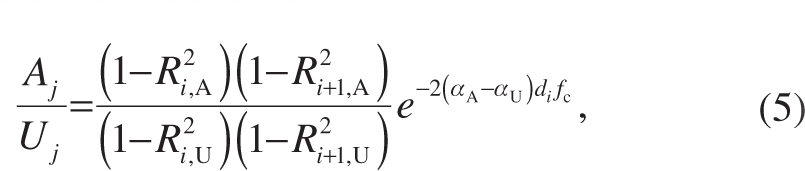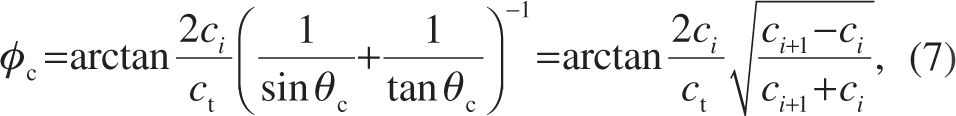Deep impact of superficial skin inking: acoustic analysis of underlying tissue
1School of Electrical and Information Engineering, University of the Witwatersrand, Johannesburg, 1 Jan Smuts Laan, 2050 Braamfontein, South Africa
2BioMediTech, Faculty of Medicine and Health Technology, Tampere University, Finland
*Correspondence to: Craig S. Carlson, E-mail: craig.carlson@wits.ac.za
Received: February 23 2021; Revised: March 22 2021; Accepted: May 8 2021; Published Online: May 31 2021
Cite this paper:
Craig S. Carlson and Michiel Postema. Deep impact of superficial skin inking: acoustic analysis of underlying tissue. BIO Integration 2021; 2(3): 109–120.
DOI: 10.15212/bioi-2021-0004. Available at: https://bio-integration.org/
Download citation
© 2021 The Authors. This is an open access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0/). See https://bio-integration.org/copyright-and-permissions/
Abstract
Background: Skin tattoos are a common decoration, but profound scientific study whether the presence of a skin tattoo alters the acoustic response from superficial tissue, and therefore from underlying tissue, was previously lacking. Any image aberrations caused by tattoo presence may have been thought negligible, yet empirically found artifacts in brightness-mode images of tattooed skin suggest otherwise. This study investigated the nature of these artifacts theoretically and experimentally in extremely simplified cases of perfectly flat and homogenous layered media and in tattooed pork.
Methods: Theory was derived for computing the acoustic response from horizontally and vertically layered media containing a thin inked layer. Experiments were performed in vitro. Artificial and pork skin were tattooed, attached to phantom material, and sonicated with a 13–6-MHz probe. The speed of sound of these materials was determined, and the perceived refraction angles was measured.
Results: The measured speeds of sound of tattooed materials were higher than those of their uninked counterparts. The presence of tattoo ink was found to have increased the linear acoustic attenuation by 1 dB/cm. This value is negligible for typical tattoos of only few millimeters. The perceived critical refraction angles of adjacent materials could be detected, and their corresponding speeds of sound were quantified. These coincided with values derived from theory.
Conclusion: The ratio of speeds of sound of adjacent materials was shown to create distinct highlights in brightness-mode images. The artifacts observed in in vitro and in vivo brightness-mode scans were explained from near-vertical transitions between areas of different sound speed. This is the first study correlating so-called critical refraction highlighting with speed-of-sound information. In addition, it was found that phantom material is a room-temperature acoustic alternative for experiments on live human skin. In summary, the presence of superficial tattoos has a small but quantifiable effect on the acoustic response from deeper tissues.
Keywords
Artificial tissue for ultrasound, critical refraction highlighting, speed of sound in skin, tattoo pigment dispersion sonication, tattooed pork, tissue-mimicking phantom.
Statement of significance
Skin tattoos are a common decoration, but profound scientific study on whether a skin tattoo alters the acoustic response from superficial tissues, and therefore from underlying tissue, was previously lacking; thus, any quantitative effects were unknown. This study was the first to investigate the nature of artifacts in ultrasound images, which have been observed to originate from tattooed skin. The work was conducted theoretically and experimentally using extremely simplified cases of perfectly flat and homogenous layered media and in tattooed pork. The measured speeds of sound of tattooed materials were higher than those of their uninked counterparts. We conclude that the artifacts observed in in vitro and in vivo brightness-mode scans were explained from near-vertical transitions between areas of different sound speeds. In addition, phantom material is a suitable acoustic alternative for live human skin. In summary, the presence of superficial tattoos has a small but quantifiable effect on the acoustic response from deeper tissues. The study integrated acoustic physics, biomaterials research, mechanical engineering, and medical imaging to increase knowledge on tattooed skin.
Introduction
Ultrasonic imaging is used for real-time medical diagnosis of internal organs and for guided delivery of therapeutics to those organs [1–4]. Although skin tattoos are a widespread and common form of permanent visible decoration, they are very rarely associated with ultrasonic imaging. In fact, with the exception of a recent in vivo study at 13–24-MHz sonication [5], subjecting inked skin to ultrasound has exclusively been performed for monitoring of dermatological tattoo complications [6, 7] and for tattoo removal [8, 9]. Ultrasonic imaging of so-called carbon-marked organ tissue is more common, however [10, 11].
To date, whether the presence of a skin tattoo alters the acoustic response from deeper underlying tissue has not been investigated. In this study, we theoretically and experimentally quantified these potential alterations. This is a relevant research topic, as novel medical treatment methods rely on quantitative data from ultrasonic images of deep tissue [12, 13]. It might be thought that ultrasonic tattoo removal requires profound knowledge on the interaction of ultrasound with inked skin. However, ultrasonic tattoo removal methods utilize high-intensity focused ultrasound [9], which heats up tissue structures [14], irrespective of presence of tattoo. Here, we focus on the effects following interaction of ultrasound with tattoo ink particles. It could be hypothesized however that the absorption of low-amplitude ultrasound by tattoo ink might lead to its disintegration.
Previous acoustic studies of hydrophobic carbon particles demonstrated nucleation at low acoustic amplitudes, but this phenomenon was found to be transient [15, 16]. As a follow-up, undiluted black tattoo ink was subjected to ultrasound in vitro. Its linear acoustic attenuation coefficient was measured to be 0.15±0.01 dB/cm/MHz, and its speed of sound in steady, non-nucleating state to be 1639 m/s [17]. Since human tissue has an average linear acoustic attenuation coefficient of 0.3 dB/cm/MHz and a speed of sound of 1540 m/s [18], one might hypothesize that the visible presence of pigment dispersion in the skin alters the pressure amplitudes of the ultrasound propagating through it. It has therefore been suggested that tattoo ink might act as a very superficial ultrasound contrast agent [19]. Yet, in tattooed tissue, the inked layer is only a few millimeters thick, reducing potential scattering and attenuation effects. Furthermore, the acoustic parameters of undiluted ink in vitro may not apply to the diluted situation in vivo.
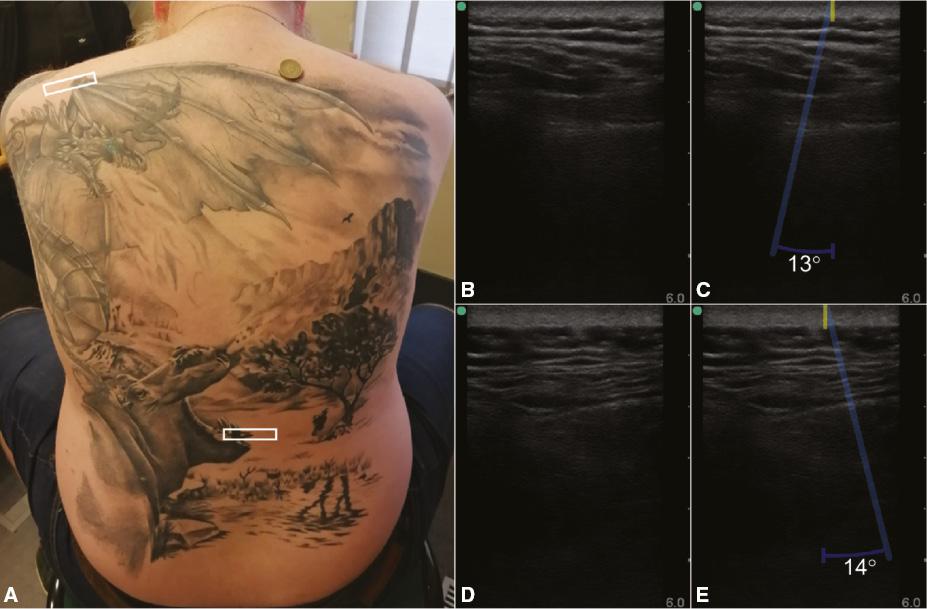
Nevertheless, the hypothesis that the presence of a superficial tattoo results in visible artifacts in brightness-mode ultrasound images has been infused by sporadic in vivo observations. Such observations are shown in Figure 1, which depicts scans of a dorsal tattoo. A highlighted region of increased scattering amplitudes from tissue transitions can be observed in both scans, originating from the separations of inked and uninked skin and directed at respective angles of 13° and 14° with respect to the normal, on the side corresponding to the uninked part.
Figure 1 Dorsal tattoo comprising carbon black and titanium white pigments. (A) The areas of the two rectangular half-inked regions of interest have been marked in white. (B) Brightness-mode image of the region of interest on the left shoulder. (C) The separation between inked and uninked skin is indicated by a yellow line, and a zone of increased scattering amplitudes is indicated by an opaque blue trapezoid. (D) Brightness-mode image of the region of interest on the lower back. (E) The separation between inked and uninked skin is indicated by a yellow line, and a zone of increased scattering amplitudes is indicated by an opaque blue trapezoid. Panels B–E have been horizontally flipped such that the left-hand side of the scan corresponds to the inked left-hand side of the region of interest. The probe was held by the same sonographer during scanning.
Such observations are rare indeed, yet this study investigates the nature of these aberrations theoretically and experimentally in extremely simplified cases of perfectly flat and homogenous layered media and in tattooed pork. The media of choice in this study have been embedded in tissue-mimicking phantoms. Phantoms are common in various medical imaging modalities, including ultrasound [20], but sonography of tissue materials embedded in tissue-mimicking phantoms, although most certainly not novel, has not been reported.
Theory
Quantitative ultrasonic imaging typically uses stochastic methods and analysis of backscattering spectral data from brightness-mode images [21–25]. In this study, we investigated absolute amplitudes from lines in such images, quite similar to early experimental work [26].
Orthogonal incidence
Let us assume a layered tissue-mimicking system with perfectly flat interfaces separating media of different acoustic impedances. Let us also assume an ultrasound field, generated and recorded by a clinical ultrasound system, whose angle of incidence coincides with the normal of the interfaces, which means that an incident ultrasound beam is orthogonal with respect to an interface plane itself. The ultrasound system converts two-way travel times to one-way radial distances, presuming a constant speed of sound through tissue ct. The one-way distances computed are henceforth referred to as perceived distances.
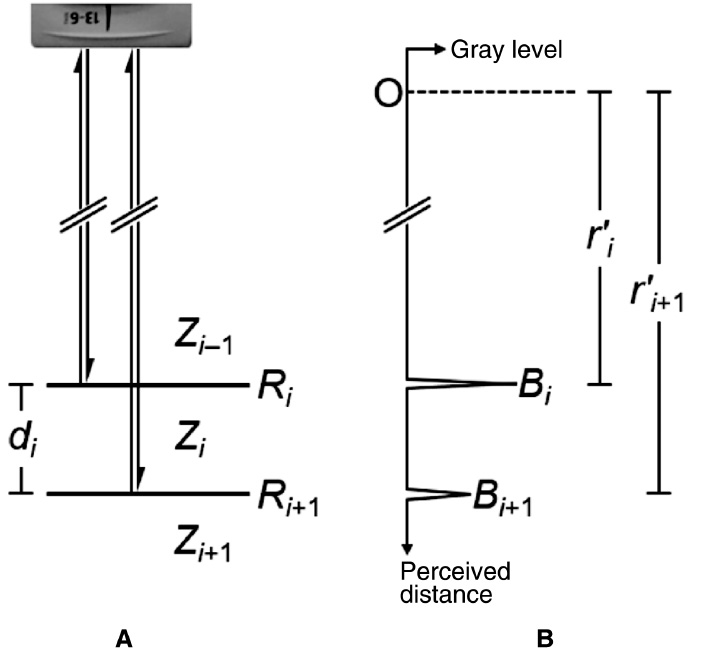
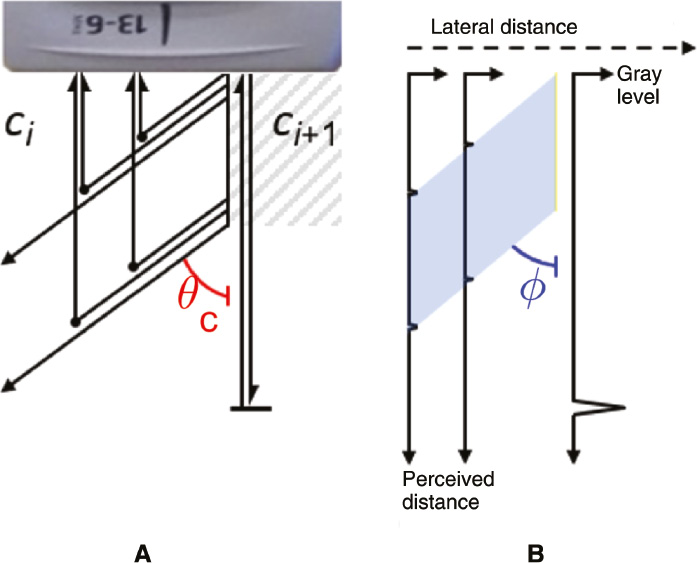
Taking into account the true tissue attenuation and the attenuation presumed by the system [18], and taking into account the dual transmission through interface i and the reflection on both respective interfaces [27], one must then find the ratio of absolute backscattered acoustic amplitudes from two adjacent interfaces i and i+1 to be
where Bi is the peak in the signal recorded from the proximal interface, Bi+1 is the peak in the signal recorded from the distal interface, di is the true thickness of the medium between the proximal and distal interfaces, fc is the center frequency of the ultrasound pulse, Ri is the reflection coefficient of the proximal interface, Ri+1 is the reflection coefficient of the distal interface, 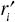
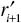
and
where ci−1, ci, and ci+1 are the respective speeds of sound in media i−1, i, and i+1; ρi−1, ρi and ρi+1 are the respective densities of the media; Zi−1, Zi, and Zi+1 are the respective acoustic impedances of the media [27].
Figure 2 Graphical representation of the parameters in Equation (1). The physical situation (A) results in an axial trace recording (B).
The unknown speed of sound of medium i of known thickness di is found from its relation to the presumed speed of sound through tissue by using
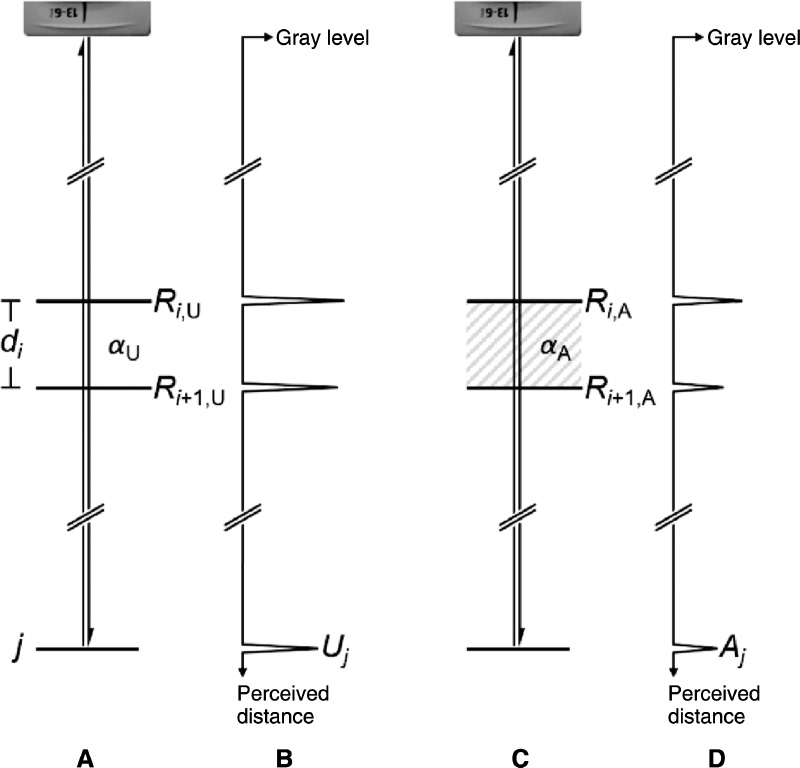
It must be noted that no prior knowledge of any medium proximal to medium i−1 is required. Equations (1)–(4) hold for any layered backscattering entity, including artificial, living, dead, and even so-called undead [29] tissues. However, without prior knowledge of media i−1, i, and i+1 themselves, the linear attenuation coefficient cannot be extracted from Equation (1), as the damping contribution from transmission and reflection cannot be quantified. Furthermore, the accuracy of computations using Equation (1) relies on the precision of determining Bi and Bi+1. If we only focus on a change in tissue properties, instead of on the tissue properties themselves, we can circumvent this issue and reduce the number of parameters as follows. The introduction of a small amount of foreign material, such as tattoo ink, in a thin medium i could slightly alter the speed of sound in the medium, causing the perceived distance from any distal interface or scatterer to shift even less slightly. However, the introduction of a foreign material should then also alter the acoustic attenuation of the medium, its density, and, consequently, the reflection coefficients of both adjacent interfaces, resulting in an alteration in the scattered amplitude from any distal interface or scatterer. Now let us consider a scatterer j at an unknown but fixed distance beyond interface i+1, whose scattering amplitude is Uj if the medium i proximal to the scatterer is unaltered, but Aj if the medium is altered. Then, the ratio of scattered amplitudes of the scatterer under these two conditions is
where the subscript A denotes altered and the subscript U denotes unaltered. A graphical representation of the parameters in Equation (5) is shown in Figure 3.
Figure 3 Graphical representation of the parameters in Equation (5). The physical situations (A, C) result in axial trace recordings (B, D).
If prior information is known about the acoustic impedances of proximal media, the difference in attenuation of altered and unaltered media can be computed from distal scattering data, using Equation (5). If no prior information is known about the acoustic impedances of proximal media, the total damping contribution Equation (5) yields the total damping contribution. Thus, the influence of ink presence is expressed by one parameter only. As a side note, in fluid media with low concentrations of materials of interest, and also in phantom materials, the contribution by the reflection coefficients has often been neglected [30–33].
Parallel incidence
Let us assume a layered tissue-mimicking system with perfectly flat interfaces, separating media of different speeds of sound. Let us also assume an ultrasound field, generated and recorded by a clinical ultrasound system, whose angle of incidence is parallel to the planes of the interfaces.
Let us consider one interface, separating two numbered media i and i+1 with respective speeds of sound of ci and ci+1. We choose our coordinate system such that ci < ci+1.
From Snell’s law, it follows that at the interface a wave front is generated with a critical refraction angle θc with respect to the incident sound field, for which
holds [27]. The scattering signals from this wave front in the direction of the probe surface are superimposed on backscattering from remote scatterers. Once the time signal received by a transducer element has been converted to one-way axial distance with respect to the receiving element and the signal amplitudes have been plotted as bright points in a brightness-mode image, the points appear to be visibly connected as if they form a highlighted trapezoid. The highlighted trapezoid has a perceived angle ϕc with respect to the normal
which has been derived from Equation (6) under the assumption that the horizontal and vertical pixel sizes of the brightness-mode image are equal. A graphical representation of the parameters in Equations (6) and (7) is shown in Figure 4.
Figure 4 Graphical representation of the parameters in Equations (6) and (7). The physical situation (A) results in axial trace recordings (B).
With the reasoning above, the ratio of the speeds of sound of two adjacent media can be derived from an ultrasound image, using only Equation (7). We refer to the phenomenon of perceived high scattering zones under an angle in brightness-mode images as critical refraction highlighting.
In case of a finite thickness of the layer with speed of sound ci, the critically refracted wave front re-refracts according to
where θr is the re-refracted angle with respect to the normal. Similar to the derivation of Equation (7), a perceived angle ϕr of the resulting trapezoid below the interface is found to be
In short, the speed of sound of inked tissue follows directly from the perceived re-refracted angle for any known tissue.
Materials and methods
Ethics
Ethical clearance was obtained from the Human Research Ethics Committee (Medical) of the University of the Witwatersrand, Johannesburg (clearance certificate no. M190808 MED19-07-006).
Preparation of tissue samples
Practice skin–silicone (yellow) measuring 30×20 cm (Body Graphics Tattoo Supply, Douglasdale, Johannesburg, South Africa) with a 3.04-mm measured thickness was used as skin-mimicking material, and a 1.104-kg piece of pork belly (Food Lover’s Market, Brackenfell, South Africa) was used to represent skin and underlying tissue.
A TM-148 Iron Shader Tattoo Machine with a 1211F standard flat needle in an 11F black disposable tattoo tube with silica gel black tattoo grip (Yuelong Tattoo Supply, Yiwu, Zhejang, China) was used to tattoo our tissue materials with Zuper Black pigment dispersion (Intenze Products, Inc., Rochelle Park, NJ, USA) until they were visibly covered. The needle was oscillating at a frequency of 100 Hz. Its penetration depth was set to 2 mm. The ink had a density of 1313 kg/m3 [17].
Sheets of artificial skin were cut into 95×65-mm2 pieces. These were tattooed with black ink or left untreated for controls. The untreated artificial skin was measured to have a density of 1087 kg/m3, whereas the inked artificial skin was measured to have a density of 1097 kg/m3. For comparison, human epidermis has a density of 1110–1190 kg/m3 [28]. The difference in thickness between inked and uninked artificial skin was reasoned to be 0.02 mm.
A 20-mm-wide strip of the pork skin was tattooed with black ink. The area next to this strip was dry-needled, i.e., tattooed without ink, so as to ensure the same skin surface as the inked part. After tattooing, the pork belly was cut into an approximately 70×45×35-mm3 cuboid, such that the 20-mm-wide black-shaded tattoo ran through the center of the skin surface.
Preparation of phantoms
Five tissue-mimicking gelatin phantoms were manufactured, one of which contained a pork belly sample. For the phantom gelatin preparation, the method described by Bude and Adler was followed [34]. Boiled tap water was allowed to cool down to 80°C before ingredients were added. A mixture of 80 g Sheridans™ Clear & Unflavoured Edible Gelatine (Libstar Operations (Pty) Ltd., Dunkeld, Johannesburg, South Africa) and 40 g psyllium husk powder (Nature’s Choice, Highbury, Randvaal, South Africa) was gradually added to a liter of water, under continuous stirring, resulting in a homogenous hydrogel.
Each phantom was produced in two steps. For the first step, 50 mL of hydrogel was poured into an HPL806 mold (LocknLock Co., Ltd., Seoul, Korea). For a phantom with tissue, the tissue sample had been placed inversely on the bottom of the mold. For a control phantom, a 27.75-mm-diameter glass 7621 20-mL VIAL 22/400 (West Pack Lifestyle, Kya Sands, Johannesburg, South Africa) or a 17.80×7.80×48.00-mm3 acrylonitrile butadiene styrene 4211075/2451 cuboid (Lego System A/S, Billund, Denmark) had been placed on the bottom of the mold. The partly filled mold was subsequently cooled at 6°C for 30 minutes.
For the second step, hydrogel was poured onto the partially set phantom. The filled mold was subsequently cooled at 6°C for 8 hours. For the control phantoms, the embedded objects were gently removed, leaving either a cylindrical or a cuboid well to be filled with distilled water for calibration purposes.
At room temperature, the resulting phantoms were 112×79×40 mm3 each. The density of the phantom material was measured to be 1025 kg/m3.
Experimental procedure
A photograph of the experimental setup in operation is shown in Figure 5. A container with inner dimension of 580×235×65 mm3, custom-made from 5-mm Plexiglas® plates (Röhm GmbH & Co. KG, Darmstadt, Germany), was filled with degassed distilled water (CJ Distribution, Glen Austin, Midrand, South Africa).
Figure 5 Experimental setup of the probe sonicating tattooed pork embedded in a tissue-mimicking phantom. According to practice [35], a St Helena £1 coin, with a diameter of 23.44 mm and thickness of 2.80 mm, has been added for scale and for three-dimensional perspective. The dimensions of the phantom were 112×79×40 mm3.
An HFL38x 13–6-MHz linear probe of a SonoSite® M-Turbo® sonography device (Fujifilm SonoSite, Inc., Bothell, WA, USA) was clamped in the length direction of the container such that the probe was underwater. There was no human interaction with the probe during the experiments.
The first side lobe of this probe has a maximum at approximately 20° with respect to the transmission axis at its center frequency [36]. An HGL-0200 S/N 1269 hydrophone (Onda Corporation, Sunnyvale, CA, USA) was placed on a 17-mm-high glass plateau such that the hydrophone was in line with and directed toward the center element of the probe, at an axial distance of 50 mm with respect to the probe surface. All objects to be investigated were individually scanned. All dimensions were calipered before and after scanning.
A tissue-mimicking phantom was positioned centrally on the bottom plane of the container, tilted such that the plane containing tissue was facing the probe surface. The probe position was not adjusted, assuring constant axial distance, azimuth, and elevation of the probe with respect to the phantom throughout the experiments.
The ultrasound system was operating in intima-media thickness or musculoskeletal pulsed brightness mode. The intima-media thickness mode was used when the tissue of interest was at an axial distance of less than 3.0 cm, and the musculoskeletal mode was used when the tissue of interest was at an axial distance greater than 3.0 cm. A single pulse comprised a chirp with frequencies of the broad bandwidth 6–13 MHz. The pulse repetition frequency was 2.5 kHz. When using control phantoms, tissue samples were positioned on the proximal side of the phantom during sonication. For controls, the tissue samples were gently removed, leaving a gap filled with distilled water between the probe and the phantom. The penetration depth of the ultrasound was set to 6.0 cm relative to the probe surface. Ultrasound pulses were indicated by the system to have a mechanical index of 0.6 and a thermal index of 0.1 [37].
Image processing
A total number of 337 brightness-mode video clips and 450 brightness-mode still-frames was recorded using the ultrasound scanner internal storage, yielding a total number greater than 15,000 brightness-mode images.
Image adjustment settings were not changed throughout the experiments. The ultrasound system was assumed to have converted two-way travel times to one-way radial distances using ct=1540 m/s for the speed of sound in tissue and to have compensated for tissue attenuation by amplifying the backscattered signal by 0.3 dB/cm/MHz.
Image processing was done using MATLAB® (The MathWorks, Inc., Natick, MA, USA). In all images recorded, the axial backscattering profiles were extracted on an 8-bit grayscale, after which the absolute peak scatter amplitudes, corresponding to the respective interfaces and individual strong scatterers, and their respective perceived distances were identified. In addition, critical refraction angles were measured manually from selected images with clear tissue transitions. The precision of measurement was 1°.
The influence of reflections and attenuation on the acoustic amplitudes was computed using Equation (5) for single distal scatterers. The speed of sound of each medium was computed from the perceived distances between peak scattering amplitudes using Equation (4) or from the perceived highlighted angle between two media using Equation (7).
Results and discussion
Table 1 shows an overview of the measured values of the speed of sound of the materials investigated. For comparison, literature values were included of media similar to those investigated.
Table 1 Measured Values of the Speed of Sound Compared with Literature Values
| Material | Measured | Compared with | Literature | References |
|---|---|---|---|---|
| c (m/s) | c (m/s) | |||
| Phantom | 1537±10 | Human skin | 1537 | [38] |
| Artificial skin | 1043±17 | Silicone rubber | 959–1113 | [39] |
| Artificial skin, tattooed | 1067±18 | Silicone rubber | 959–1113 | [39] |
| Pork skin, dry-needled | 1508±2 | Pig skin | 1503 | [40] |
| Pork skin, tattooed | 1509±3 | Pig skin | 1503 | [40] |
The phantom material had a speed of sound at room temperature equal to that of human skin at body temperature [38]. The speed of sound in inked artificial skin was greater than in uninked skin, but the error bars overlapped. Both values are in the range found in literature for its primary component [39]. Despite the near-matching density of artificial skin, its speed of sound is not representative for human skin at all.
In pork skin, no significant difference in the speed of sound was measured between the inked and uninked skin, based on 640 brightness-mode images. The mean value pork skin at room temperature of 1508±2 m/s is close to the literature value of pig skin at body temperature of 1503 m/s [40]. It has been reported that storage increases the speed of sound of meat over time [40], which might account for the minor difference.
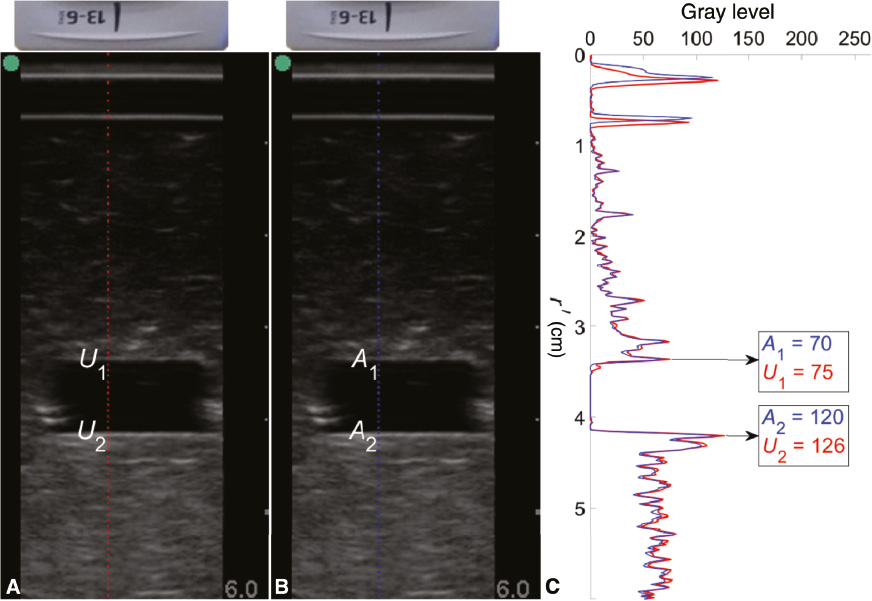
Figure 6 shows an example of brightness-mode images of artificial skin positioned between the ultrasound probe and a control phantom with a cuboid space filled with distilled water. From the axial grayscale profile of unaltered skin, the peak backscattered value U1 representing the phantom–water interface and U2 representing the water–phantom interface were found to be 75 and 126, respectively. From the axial grayscale profile of tattooed skin, the peak backscattered value A1 representing the phantom–water interface and A2 representing the water–phantom interface were found to be 70 and 120, respectively.
Figure 6 Brightness-mode scans of artificial skin, unaltered (A) and altered by tattooing (B), positioned proximal to phantom material and their respective axial grayscale profiles (C).
Knowing the respective reflection coefficients, the difference in attenuation between inked and unaltered skin followed from Equation (5), which had been applied to 1206 brightness-mode images. Using the backscattering amplitude from either interface, the 1-dB/cm difference caused by the presence of tattoo ink is negligible, knowing that the thickness of the tattooed layer is only a few millimeters. This finding would also suggest that ultrasonic tattoo removal at low acoustic amplitudes is not feasible in the frequency range investigated, but this is beyond the scope of the present study.
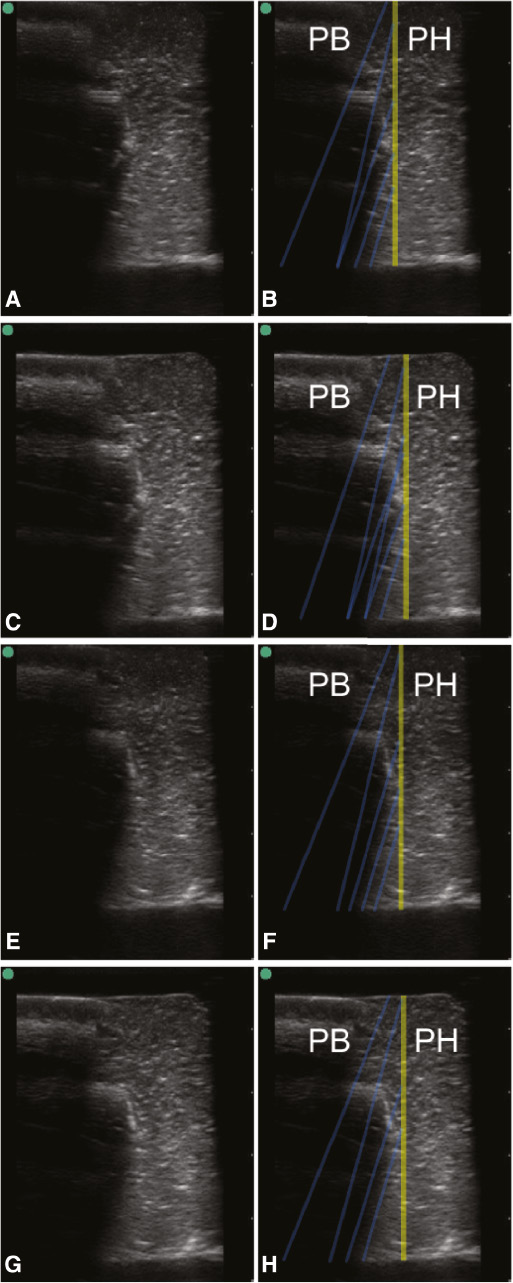
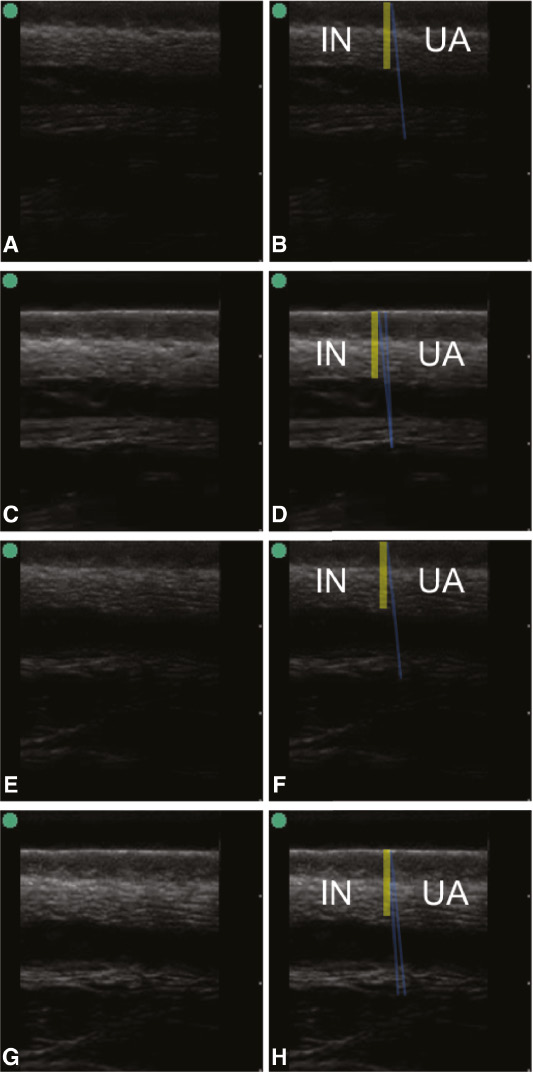
A few representative examples of critical refraction highlighting are demonstrated in Figure 7 and 8. These serve to illustrate theory and practical limitations. Figure 7 shows four representative proof-of-principle scans of pork belly adjacent to phantom material, from a subset of 468 brightness-mode images. The perceived angles of the multiple highlighted regions were seen to vary between 10° and 21°. Taking into account the error margins of both materials, we computed the angles for the ratio of the speeds of sound of phantom and pork skin between 9° and 14°. However, if we also include the speed of sound of pig fat, 1426 m/s, in Equation (7), the greatest theoretical angle is 24°. Consequently, our measurements on pork belly fell inside the theoretical margin. This control experiment showed that regions were highlighted in brightness-mode images if adjacent materials have a different speed of sound.
Figure 7 Unmarked (A, C, E, G) and marked (B, D, F, H) brightness-mode scan of pork belly (PB) adjacent to phantom material (PH). The separation between pork and phantom material is indicated by a yellow line and zones of increased scattering amplitudes by opaque blue lines.
Figure 8 Unmarked (A, C, E, G) and marked (B, D, F, H) brightness-mode scan of inked pork belly (IN) and unaltered pork belly (UA). The separation between inked and uninked skin is indicated by a yellow line and zones of increased scattering amplitudes by opaque blue lines.
Figure 8 shows another four representative scans of embedded pork of the transition between inked and uninked skin from a subset of 394 brightness-mode images. Here, the perceived angles deviated from the normal by 6° or less. Taking into account the standard deviation of the speed of sound of pork skin (cf. Table 1), which had been measured from 640 brightness-mode images, the perceived angle should lie between 2° and 5°. Although the highlighted areas confirm the theory, determining the angles is too subjective to draw firm conclusions.
Revisiting Figure 1, presuming a speed of sound of 1537 m/s in the uninked skin of the subject and a critical refraction angle of 13°–14°, Equation (7) yields a speed of sound of the inked skin of 1579–1586 m/s, suggesting a high ink concentration. This speed of sound difference between inked and uninked skin cannot be observed from the thicknesses of the dermis, as the perceived difference in thickness of the approximately 2-mm tattooed layer would be only 0.06 mm. Furthermore, it is noted that, in this case, a 1° measurement difference in the critical refraction angle leads to a rather insignificant difference in sound speed of 7 m/s.
Although critical refraction highlighting has shown plausible speed-of-sound ratios in the simplified situations presented in this study, an inherent flaw is the measurement error in the perceived angle. By defining scattering brightness criteria and automating the highlighted region selection and measurement, the precision might be improved.
Our interest was primarily focused on subsurface acoustic effects resulting from superficial skin tattoos, but critical refraction highlighting might be applied in fields where the detection of vertically layered media with high speed-of-sound differences is crucial. These might include the identification of near-surface tissue types, the nondestructive detection of construction flaws, and even the detection and identification of geological trap constructions.
The ultrasound frequencies generated by the probe used in this study were high enough to detect tissue transitions but low enough to avoid scattering from skin inhomogeneities. As the purpose of this study was to quantify acoustic effects of superficial skin inking on deeper structures, the choice of the probe used was justified.
Despite its straightforward approach, the embedding of tissues in phantom for quantitative ultrasonic imaging has been novel.
As for the theoretical considerations, we have used straightforward derivations to deduce acoustic properties of tissues and tissue-mimicking materials from grayscale values in brightness-mode images. Although this idea may not come across as novel, literature on this topic has been sparse, possibly because some commercial ultrasound equipment does not represent brightness-mode images on a linear grayscale. Thus, our study has shown benefits of ultrasound equipment without automatic gain control and other image adjustment features.
Conclusions
Phantom material at room temperature has the same speed of sound as human skin at body temperature. It is therefore a potential alternative for acoustic experiments on skin at lower-than-body temperatures. To our knowledge, no other materials have been proposed for this purpose. The ratio in speeds of sound of adjacent materials was shown to create distinct highlights in brightness-mode images. The artifacts observed in in vivo brightness-mode scans might be explained from vertical transitions between inked and uninked skin areas. No prior study has reported the correlation of critical refraction highlighting with the speed of sound of adjacent materials. This finding is useful for the quantification from brightness-mode ultrasound images of tissue structures deep underneath inked skin in particular, as well as for the detection and identification of adjacent media in general from such images.
Acknowledgements
The sonography equipment was kindly supplied by High Tech Medical, Randburg, South Africa. This work has been based on research supported in part by the National Research Foundation of South Africa (grant number 127102).
References
- Huang P. An integrated approach to ultrasound imaging in medicine and biology. BIO Integration 2020;1:105-9. [DOI: 10.15212/bioi-2020-0036]
- Piscaglia F, Stefanini F, Cantisani V, Sidhu PS, Barr R, et al. Benefits, Open questions and challenges of the use of ultrasound in the COVID-19 pandemic era: the views of a panel of worldwide international experts. Ultraschall Med 2020;41:228-36. [PMID: 32294795 DOI: 10.1055/a-1149-9872]
- Yang Y, Li Q, Guo X, Tu J, Zhang D. Mechanisms underlying sonoporation: interaction between microbubbles and cells. Ultrason Sonochem 2020;67:105096. [DOI: 10.1016/j.ultsonch.2020.105096]
- Zhang T, Wu B, Akakuru OU, Yao C, Sun S, et al. Hsp90 inhibitor-loaded IR780 micelles for mitochondria-targeted mild-temperature photothermal therapy in xenograft models of human breast cancer. Cancer Lett. 2021;500:41-50. [PMID: 33359275 DOI: 10.1016/j.canlet.2020.12.028]
- Rajab Bolookat E, Rich LJ, Paragh G, Colegio OR, Singh AK, et al. Photoacoustic imaging of tattoo inks: phantom and clinical evaluation. Appl Sci 2020;10:1024. [PMID: 33604062 DOI: 10.3390/app10031024]
- Hutton Carlsen K, Tolstrup J, Serup J. High-frequency ultrasound imaging of tattoo reactions with histopathology as a comparative method: introduction of preoperative ultrasound diagnostics as a guide to therapeutic intervention. Skin Res Technol 2014;20:257-64. [PMID: 24010847 DOI: 10.1111/srt.12110]
- Serup J. Diagnostic tools for doctor’s evaluation of tattoo complications. Curr Probl Dermatol 2017;52:42-57. [PMID: 28288455 DOI: 10.1159/000450778]
- Hazlewood D, Yang X. Enhanced laser surface ablation with an integrated photoacoustic imaging and high intensity focused ultrasound system. Lasers Surg Med 2019;51:616-24. [PMID: 30860297 DOI: 10.1002/lsm.23072]
- Serup J, Bove T, Zawada T, Jessen A, Poli M. High-frequency (20 MHz) high-intensity focused ultrasound: new ablative method for color-independent tattoo removal in 1–3 sessions. An open-label exploratory study. Skin Res Technol 2020;26:839-50. [PMID: 32557859 DOI: 10.1111/srt.12885]
- Matsuda T, Iwasaki T, Hirata K, Tsugawa D, Sugita Y, et al. Simple and reliable method for tumor localization during totally laparoscopic gastrectomy: intraoperative laparoscopic ultrasonography combined with tattooing. Gastric Cancer 2017;20:548-52. [PMID: 27539582 DOI: 10.1007/s10120-016-0635-z]
- Hartmann S, Kuhn T, de Boniface J, Stachs A, Winckelmann A, et al. Carbon tattooing for targeted lymph node biopsy after primary systemic therapy in breast cancer: prospective multicentre TATTOO trial. Br J Surg 2021;108:302-7. [PMID: 33793745 DOI: 10.1093/bjs/znaa083]
- Kotopoulis S, Delalande A, Popa M, Mamaeva V, Dimcevski G, et al. Sonoporation-enhanced chemotherapy significantly reduces primary tumour burden in an orthotopic pancreatic cancer xenograft. Mol Imaging Biol 2014;16:53-62. [PMID: 23877869 DOI: 10.1007/s11307-013-0672-5]
- Dimcevski G, Kotopoulis S, Bjånes T, Hoem D, Schjøtt J, et al. A human clinical trial using ultrasound and microbubbles to enhance gemcitabine treatment of inoperable pancreatic cancer. J Control Release 2016;243:172-81. [PMID: 27744037 DOI: 10.1016/j.jconrel.2016.10.007]
- ter Haar G. HIFU tissue ablation: concept and devices. Adv Exp Med Biol 2016;880:3-20. [DOI: 10.1007/978-3-319-22536-4_1]
- Carlson CS, Matsumoto R, Fushino K, Shinzato M, Kudo N, et al. Transient ink nucleation: the proof is in the pudding. Proc 41st UltraSonic Electronics Symp 2020:2E5-1.
- Postema M, Matsumoto R, Shimizu R, Poortinga AT, Kudo N. High-speed footage shows transient ultrasonic nucleation of different hydrophobic particles in suspension. Jpn J Appl Phys 2020;59:SKKD07. [DOI: 10.35848/1347-4065/ab7f19]
- Carlson CS, Deroubaix A, Penny C, Postema M. On the attenuation of pure black tattoo ink. SAIEE Afr Res J 2021;112:24-31. [DOI: 10.23919/SAIEE.2021.9340534]
- ter Haar G. Ultrasonic imaging: safety considerations. Interface Focus 2011;1:686-97. [PMID: 22866238 DOI: 10.1098/rsfs.2011.0029]
- Carlson CS, Matsumoto R, Fushino K, Shinzato M, Kudo N, Postema M. Nucleation threshold of carbon black ultrasound contrast agent. Jpn J Appl Phys 2021;60:SDDA06. [DOI: 10.35848/1347-4065/abef0f]
- Hofstetter LW, Fausett L, Mueller A, Odéen H, Payne A, et al. Development and characterization of a tissue mimicking psyllium husk gelatin phantom for ultrasound and magnetic resonance imaging. Int J Hyperthermia 2020;37:283-90. [PMID: 32204632 DOI: 10.1080/02656736.2020.1739345]
- Tsui PH, Shu YC, Chen WS, Liu HL, Hsiao IT, et al. Ultrasound temperature estimation based on probability variation of backscatter data. Med Phys 2012;39:2369-85. [PMID: 22559607 DOI: 10.1118/1.3700235]
- Oelze ML, Mamou J. Review of quantitative ultrasound: envelope statistics and backscatter coefficient imaging and contributions to diagnostic ultrasound. IEEE Trans Ultrason Ferroelectr Freq Control 2016;63:336-51. [PMID: 26761606 DOI: 10.1109/TUFFC.2015.2513958]
- Han A, Zhang YN, Boehringer AS, Andre MP, Erdman JW Jr, et al. Inter-platform reproducibility of ultrasonic attenuation and backscatter coefficients in assessing NAFLD. Eur Radiol 2019;29:4699-708. [PMID: 30783789 DOI: 10.1007/s00330-019-06035-9]
- Omura M, Hasegawa H, Nagaoka R, Yoshida K, Yamaguchi T. Validation of differences in backscatter coefficients among four ultrasound scanners with different beamforming methods. J Med Ultrason 2020;47:35-46. [PMID: 31679096 DOI: 10.1007/s10396-019-00984-w]
- Iori G, Du J, Hackenbeck J, Kilappa V, Raum K. Estimation of cortical bone microstructure from ultrasound backscatter. IEEE Trans Ultrason Ferroelectr Freq Control 2021;68:1081-95. [PMID: 33104498 DOI: 10.1109/TUFFC.2020.3033050]
- Lopez H, Harris KM. Ultrasound interactions with free silicone in a tissue-mimicking phantom. J Ultrasound Med 1998;17:163-70. [PMID: 9514168 DOI: 10.7863/jum.1998.17.3.163]
- Postema M. Fundamentals of medical ultrasonics. London, UK: Taylor & Francis; 2011. [DOI: 10.1201/9781482266641]
- Duck FA. Physical properties of tissue: a comprehensive reference book. London, UK: Academic Press; 1990. [DOI: 10.1016/C2009-0-02755-X]
- Ressel L. The biopsy “undead”. Vet Pathol 2018;55:916-7. [PMID: 30381035 DOI: 10.1177/0300985818789478]
- Kuc R, Schwartz M. Estimating the acoustic attenuation coefficient slope for liver from reflected ultrasound signals. IEEE Trans on Sonics Ultrason 1979;26:353-61. [DOI: 10.1109/T-SU.1979.31116]
- Hensel K, Schmitz G. Method for the estimation and compensation of attenuating tissue layers by the acoustic observation of microbubbles for sonoporation therapy. Proc 2010 IEEE Int Ultrason Symp 2010:1700-3. [DOI: 10.1109/ULTSYM.2010.0431]
- Perlman O, Azhari H. Ultrasonic computed tomography imaging of iron oxide nanoparticles. Phys Med Biol 2017;62:825-42. [PMID: 28072576 DOI: 10.1088/1361-6560/aa51ab]
- Alves N, Kim A, Tan J, Hwang G, Javed T, et al. Cardiac tissue-mimicking ballistic gel phantom for ultrasound imaging in clinical and research applications. Ultrasound Med Biol 2020;46:2057-69. [PMID: 32430107 DOI: 10.1016/j.ultrasmedbio.2020.03.011]
- Bude RO, Adler RS. An easily made, low-cost, tissue-like ultrasound phantom material. J Clin Ultrasound 1995;23:271-3. [PMID: 7797668 DOI: 10.1002/jcu.1870230413]
- Stanway P, Nudds J, Broadhurst F. The depositional environment of the Ashfell Sandstone Formation (Arundian, Mississippian), Ash Fell Edge, Cumbria, NW England. Proc Yorkshire Geol Soc 2015;60:145-52. [DOI: 10.1144/pygs2015-344]
- Krautkrämer J, Krautkrämer H. Werkstoffprüfung mit Ultraschall. 5th ed. Berlin, Germany: Springer; 1986. [DOI: 10.1007/978-3-662-10909-0]
- Nowicki A. Safety of ultrasonic examinations; thermal and mechanical indices. Med Ultrason 2020;22:203-10. [PMID: 32399527 DOI: 10.11152/mu-2372]
- Yongchen S, Yanwu D, Jie T, Zhensheng T. Ultrasonic propagation parameters in human tissues. Proc IEEE Ultrason Symp 1986:905-8. [DOI: 10.1109/ULTSYM.1986.198866]
- Folds DL. Speed of sound and transmission loss in silicone rubbers at ultrasonic frequencies. J Acoust Soc Am 1974;56:1295-6. [DOI: 10.1121/1.1903422]
- Lewin P, Busk H. In vivo ultrasonic measurements of tissue properties. Proc IEEE Ultrason Symp 1982:709-12. [DOI: 10.1109/ULTSYM.1982.197922]